Learning to tokenize in Vision Transformers
Authors: Aritra Roy Gosthipaty, Sayak Paul (equal contribution), converted to Keras 3 by Muhammad Anas Raza
Date created: 2021/12/10
Last modified: 2023/08/14
Description: Adaptively generating a smaller number of tokens for Vision Transformers.
Introduction
Vision Transformers (Dosovitskiy et al.) and many other Transformer-based architectures (Liu et al., Yuan et al., etc.) have shown strong results in image recognition. The following provides a brief overview of the components involved in the Vision Transformer architecture for image classification:
- Extract small patches from input images.
- Linearly project those patches.
- Add positional embeddings to these linear projections.
- Run these projections through a series of Transformer (Vaswani et al.) blocks.
- Finally, take the representation from the final Transformer block and add a classification head.
If we take 224x224 images and extract 16x16 patches, we get a total of 196 patches (also called tokens) for each image. The number of patches increases as we increase the resolution, leading to higher memory footprint. Could we use a reduced number of patches without having to compromise performance? Ryoo et al. investigate this question in TokenLearner: Adaptive Space-Time Tokenization for Videos. They introduce a novel module called TokenLearner that can help reduce the number of patches used by a Vision Transformer (ViT) in an adaptive manner. With TokenLearner incorporated in the standard ViT architecture, they are able to reduce the amount of compute (measured in FLOPS) used by the model.
In this example, we implement the TokenLearner module and demonstrate its performance with a mini ViT and the CIFAR-10 dataset. We make use of the following references:
- Official TokenLearner code
- Image Classification with ViTs on keras.io
- TokenLearner slides from NeurIPS 2021
Imports
import keras
from keras import layers
from keras import ops
from tensorflow import data as tf_data
from datetime import datetime
import matplotlib.pyplot as plt
import numpy as np
import math
Hyperparameters
Please feel free to change the hyperparameters and check your results. The best way to develop intuition about the architecture is to experiment with it.
# DATA
BATCH_SIZE = 256
AUTO = tf_data.AUTOTUNE
INPUT_SHAPE = (32, 32, 3)
NUM_CLASSES = 10
# OPTIMIZER
LEARNING_RATE = 1e-3
WEIGHT_DECAY = 1e-4
# TRAINING
EPOCHS = 1
# AUGMENTATION
IMAGE_SIZE = 48 # We will resize input images to this size.
PATCH_SIZE = 6 # Size of the patches to be extracted from the input images.
NUM_PATCHES = (IMAGE_SIZE // PATCH_SIZE) ** 2
# ViT ARCHITECTURE
LAYER_NORM_EPS = 1e-6
PROJECTION_DIM = 128
NUM_HEADS = 4
NUM_LAYERS = 4
MLP_UNITS = [
PROJECTION_DIM * 2,
PROJECTION_DIM,
]
# TOKENLEARNER
NUM_TOKENS = 4
Load and prepare the CIFAR-10 dataset
# Load the CIFAR-10 dataset.
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
(x_train, y_train), (x_val, y_val) = (
(x_train[:40000], y_train[:40000]),
(x_train[40000:], y_train[40000:]),
)
print(f"Training samples: {len(x_train)}")
print(f"Validation samples: {len(x_val)}")
print(f"Testing samples: {len(x_test)}")
# Convert to tf.data.Dataset objects.
train_ds = tf_data.Dataset.from_tensor_slices((x_train, y_train))
train_ds = train_ds.shuffle(BATCH_SIZE * 100).batch(BATCH_SIZE).prefetch(AUTO)
val_ds = tf_data.Dataset.from_tensor_slices((x_val, y_val))
val_ds = val_ds.batch(BATCH_SIZE).prefetch(AUTO)
test_ds = tf_data.Dataset.from_tensor_slices((x_test, y_test))
test_ds = test_ds.batch(BATCH_SIZE).prefetch(AUTO)
Training samples: 40000
Validation samples: 10000
Testing samples: 10000
Data augmentation
The augmentation pipeline consists of:
- Rescaling
- Resizing
- Random cropping (fixed-sized or random sized)
- Random horizontal flipping
data_augmentation = keras.Sequential(
[
layers.Rescaling(1 / 255.0),
layers.Resizing(INPUT_SHAPE[0] + 20, INPUT_SHAPE[0] + 20),
layers.RandomCrop(IMAGE_SIZE, IMAGE_SIZE),
layers.RandomFlip("horizontal"),
],
name="data_augmentation",
)
Note that image data augmentation layers do not apply data transformations at inference time.
This means that when these layers are called with training=False they behave differently. Refer
to the documentation for more
details.
Positional embedding module
A Transformer architecture consists of multi-head self attention layers and fully-connected feed forward networks (MLP) as the main components. Both these components are permutation invariant: they're not aware of feature order.
To overcome this problem we inject tokens with positional information. The
position_embedding function adds this positional information to the linearly projected
tokens.
class PatchEncoder(layers.Layer):
def __init__(self, num_patches, projection_dim):
super().__init__()
self.num_patches = num_patches
self.position_embedding = layers.Embedding(
input_dim=num_patches, output_dim=projection_dim
)
def call(self, patch):
positions = ops.expand_dims(
ops.arange(start=0, stop=self.num_patches, step=1), axis=0
)
encoded = patch + self.position_embedding(positions)
return encoded
def get_config(self):
config = super().get_config()
config.update({"num_patches": self.num_patches})
return config
MLP block for Transformer
This serves as the Fully Connected Feed Forward block for our Transformer.
def mlp(x, dropout_rate, hidden_units):
# Iterate over the hidden units and
# add Dense => Dropout.
for units in hidden_units:
x = layers.Dense(units, activation=ops.gelu)(x)
x = layers.Dropout(dropout_rate)(x)
return x
TokenLearner module
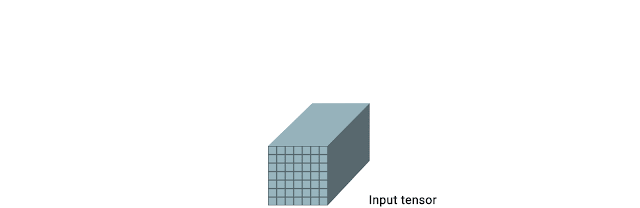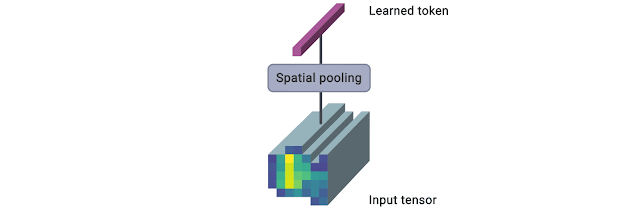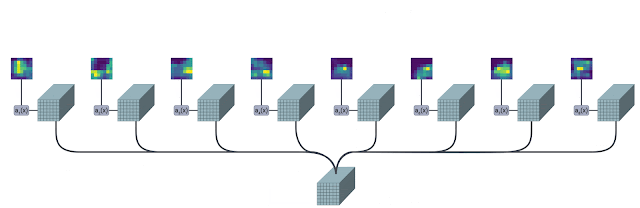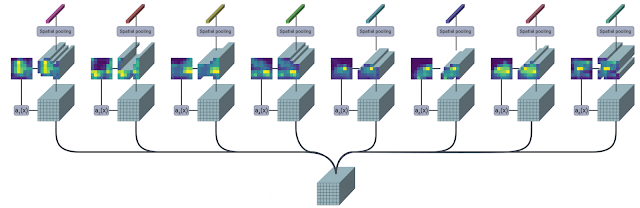
The following figure presents a pictorial overview of the module (source).
The TokenLearner module takes as input an image-shaped tensor. It then passes it through multiple single-channel convolutional layers extracting different spatial attention maps focusing on different parts of the input. These attention maps are then element-wise multiplied to the input and result is aggregated with pooling. This pooled output can be trated as a summary of the input and has much lesser number of patches (8, for example) than the original one (196, for example).
Using multiple convolution layers helps with expressivity. Imposing a form of spatial attention helps retain relevant information from the inputs. Both of these components are crucial to make TokenLearner work, especially when we are significantly reducing the number of patches.
def token_learner(inputs, number_of_tokens=NUM_TOKENS):
# Layer normalize the inputs.
x = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(inputs) # (B, H, W, C)
# Applying Conv2D => Reshape => Permute
# The reshape and permute is done to help with the next steps of
# multiplication and Global Average Pooling.
attention_maps = keras.Sequential(
[
# 3 layers of conv with gelu activation as suggested
# in the paper.
layers.Conv2D(
filters=number_of_tokens,
kernel_size=(3, 3),
activation=ops.gelu,
padding="same",
use_bias=False,
),
layers.Conv2D(
filters=number_of_tokens,
kernel_size=(3, 3),
activation=ops.gelu,
padding="same",
use_bias=False,
),
layers.Conv2D(
filters=number_of_tokens,
kernel_size=(3, 3),
activation=ops.gelu,
padding="same",
use_bias=False,
),
# This conv layer will generate the attention maps
layers.Conv2D(
filters=number_of_tokens,
kernel_size=(3, 3),
activation="sigmoid", # Note sigmoid for [0, 1] output
padding="same",
use_bias=False,
),
# Reshape and Permute
layers.Reshape((-1, number_of_tokens)), # (B, H*W, num_of_tokens)
layers.Permute((2, 1)),
]
)(
x
) # (B, num_of_tokens, H*W)
# Reshape the input to align it with the output of the conv block.
num_filters = inputs.shape[-1]
inputs = layers.Reshape((1, -1, num_filters))(inputs) # inputs == (B, 1, H*W, C)
# Element-Wise multiplication of the attention maps and the inputs
attended_inputs = (
ops.expand_dims(attention_maps, axis=-1) * inputs
) # (B, num_tokens, H*W, C)
# Global average pooling the element wise multiplication result.
outputs = ops.mean(attended_inputs, axis=2) # (B, num_tokens, C)
return outputs
Transformer block
def transformer(encoded_patches):
# Layer normalization 1.
x1 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(encoded_patches)
# Multi Head Self Attention layer 1.
attention_output = layers.MultiHeadAttention(
num_heads=NUM_HEADS, key_dim=PROJECTION_DIM, dropout=0.1
)(x1, x1)
# Skip connection 1.
x2 = layers.Add()([attention_output, encoded_patches])
# Layer normalization 2.
x3 = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(x2)
# MLP layer 1.
x4 = mlp(x3, hidden_units=MLP_UNITS, dropout_rate=0.1)
# Skip connection 2.
encoded_patches = layers.Add()([x4, x2])
return encoded_patches
ViT model with the TokenLearner module
def create_vit_classifier(use_token_learner=True, token_learner_units=NUM_TOKENS):
inputs = layers.Input(shape=INPUT_SHAPE) # (B, H, W, C)
# Augment data.
augmented = data_augmentation(inputs)
# Create patches and project the pathces.
projected_patches = layers.Conv2D(
filters=PROJECTION_DIM,
kernel_size=(PATCH_SIZE, PATCH_SIZE),
strides=(PATCH_SIZE, PATCH_SIZE),
padding="VALID",
)(augmented)
_, h, w, c = projected_patches.shape
projected_patches = layers.Reshape((h * w, c))(
projected_patches
) # (B, number_patches, projection_dim)
# Add positional embeddings to the projected patches.
encoded_patches = PatchEncoder(
num_patches=NUM_PATCHES, projection_dim=PROJECTION_DIM
)(
projected_patches
) # (B, number_patches, projection_dim)
encoded_patches = layers.Dropout(0.1)(encoded_patches)
# Iterate over the number of layers and stack up blocks of
# Transformer.
for i in range(NUM_LAYERS):
# Add a Transformer block.
encoded_patches = transformer(encoded_patches)
# Add TokenLearner layer in the middle of the
# architecture. The paper suggests that anywhere
# between 1/2 or 3/4 will work well.
if use_token_learner and i == NUM_LAYERS // 2:
_, hh, c = encoded_patches.shape
h = int(math.sqrt(hh))
encoded_patches = layers.Reshape((h, h, c))(
encoded_patches
) # (B, h, h, projection_dim)
encoded_patches = token_learner(
encoded_patches, token_learner_units
) # (B, num_tokens, c)
# Layer normalization and Global average pooling.
representation = layers.LayerNormalization(epsilon=LAYER_NORM_EPS)(encoded_patches)
representation = layers.GlobalAvgPool1D()(representation)
# Classify outputs.
outputs = layers.Dense(NUM_CLASSES, activation="softmax")(representation)
# Create the Keras model.
model = keras.Model(inputs=inputs, outputs=outputs)
return model
As shown in the TokenLearner paper, it is almost always advantageous to include the TokenLearner module in the middle of the network.
Training utility
def run_experiment(model):
# Initialize the AdamW optimizer.
optimizer = keras.optimizers.AdamW(
learning_rate=LEARNING_RATE, weight_decay=WEIGHT_DECAY
)
# Compile the model with the optimizer, loss function
# and the metrics.
model.compile(
optimizer=optimizer,
loss="sparse_categorical_crossentropy",
metrics=[
keras.metrics.SparseCategoricalAccuracy(name="accuracy"),
keras.metrics.SparseTopKCategoricalAccuracy(5, name="top-5-accuracy"),
],
)
# Define callbacks
checkpoint_filepath = "/tmp/checkpoint.weights.h5"
checkpoint_callback = keras.callbacks.ModelCheckpoint(
checkpoint_filepath,
monitor="val_accuracy",
save_best_only=True,
save_weights_only=True,
)
# Train the model.
_ = model.fit(
train_ds,
epochs=EPOCHS,
validation_data=val_ds,
callbacks=[checkpoint_callback],
)
model.load_weights(checkpoint_filepath)
_, accuracy, top_5_accuracy = model.evaluate(test_ds)
print(f"Test accuracy: {round(accuracy * 100, 2)}%")
print(f"Test top 5 accuracy: {round(top_5_accuracy * 100, 2)}%")
Train and evaluate a ViT with TokenLearner
vit_token_learner = create_vit_classifier()
run_experiment(vit_token_learner)
157/157 ━━━━━━━━━━━━━━━━━━━━ 303s 2s/step - accuracy: 0.1158 - loss: 2.4798 - top-5-accuracy: 0.5352 - val_accuracy: 0.2206 - val_loss: 2.0292 - val_top-5-accuracy: 0.7688
40/40 ━━━━━━━━━━━━━━━━━━━━ 5s 133ms/step - accuracy: 0.2298 - loss: 2.0179 - top-5-accuracy: 0.7723
Test accuracy: 22.9%
Test top 5 accuracy: 77.22%
Results
We experimented with and without the TokenLearner inside the mini ViT we implemented (with the same hyperparameters presented in this example). Here are our results:
| TokenLearner | # tokens in TokenLearner |
Top-1 Acc (Averaged across 5 runs) |
GFLOPs | TensorBoard |
|---|---|---|---|---|
| N | - | 56.112% | 0.0184 | Link |
| Y | 8 | 56.55% | 0.0153 | Link |
| N | - | 56.37% | 0.0184 | Link |
| Y | 4 | 56.4980% | 0.0147 | Link |
| N | - (# Transformer layers: 8) | 55.36% | 0.0359 | Link |
TokenLearner is able to consistently outperform our mini ViT without the module. It is also interesting to notice that it was also able to outperform a deeper version of our mini ViT (with 8 layers). The authors also report similar observations in the paper and they attribute this to the adaptiveness of TokenLearner.
One should also note that the FLOPs count decreases considerably with the addition of the TokenLearner module. With less FLOPs count the TokenLearner module is able to deliver better results. This aligns very well with the authors' findings.
Additionally, the authors introduced a newer version of the TokenLearner for smaller training data regimes. Quoting the authors:
Instead of using 4 conv. layers with small channels to implement spatial attention, this version uses 2 grouped conv. layers with more channels. It also uses softmax instead of sigmoid. We confirmed that this version works better when having limited training data, such as training with ImageNet1K from scratch.
We experimented with this module and in the following table we summarize the results:
| # Groups | # Tokens | Top-1 Acc | GFLOPs | TensorBoard |
|---|---|---|---|---|
| 4 | 4 | 54.638% | 0.0149 | Link |
| 8 | 8 | 54.898% | 0.0146 | Link |
| 4 | 8 | 55.196% | 0.0149 | Link |
Please note that we used the same hyperparameters presented in this example. Our implementation is available in this notebook. We acknowledge that the results with this new TokenLearner module are slightly off than expected and this might mitigate with hyperparameter tuning.
Note: To compute the FLOPs of our models we used this utility from this repository.
Number of parameters
You may have noticed that adding the TokenLearner module increases the number of parameters of the base network. But that does not mean it is less efficient as shown by Dehghani et al.. Similar findings were reported by Bello et al. as well. The TokenLearner module helps reducing the FLOPS in the overall network thereby helping to reduce the memory footprint.
Final notes
- TokenFuser: The authors of the paper also propose another module named TokenFuser. This module helps in remapping the representation of the TokenLearner output back to its original spatial resolution. To reuse the TokenLearner in the ViT architecture, the TokenFuser is a must. We first learn the tokens from the TokenLearner, build a representation of the tokens from a Transformer layer and then remap the representation into the original spatial resolution, so that it can again be consumed by a TokenLearner. Note here that you can only use the TokenLearner module once in entire ViT model if not paired with the TokenFuser.
- Use of these modules for video: The authors also suggest that TokenFuser goes really well with Vision Transformers for Videos (Arnab et al.).
We are grateful to JarvisLabs and Google Developers Experts program for helping with GPU credits. Also, we are thankful to Michael Ryoo (first author of TokenLearner) for fruitful discussions.