» Code examples / Quick Keras Recipes / Keras debugging tips

Keras debugging tips

Author: fchollet
Date created: 2020/05/16
Last modified: 2020/05/16
Description: Four simple tips to help you debug your Keras code.

View in Colab • GitHub source

Introduction

It's generally possible to do almost anything in Keras without writing code per se: whether you're implementing a new type of GAN or the latest convnet architecture for image segmentation, you can usually stick to calling built-in methods. Because all built-in methods do extensive input validation checks, you will have little to no debugging to do. A Functional API model made entirely of built-in layers will work on first try -- if you can compile it, it will run.

However, sometimes, you will need to dive deeper and write your own code. Here are some common examples:

  • Creating a new Layer subclass.
  • Creating a custom Metric subclass.
  • Implementing a custom train_step on a Model.

This document provides a few simple tips to help you navigate debugging in these situations.

Tip 1: test each part before you test the whole

If you've created any object that has a chance of not working as expected, don't just drop it in your end-to-end process and watch sparks fly. Rather, test your custom object in isolation first. This may seem obvious -- but you'd be surprised how often people don't start with this.

  • If you write a custom layer, don't call fit() on your entire model just yet. Call your layer on some test data first.
  • If you write a custom metric, start by printing its output for some reference inputs.

Here's a simple example. Let's write a custom layer a bug in it:

import tensorflow as tf
from tensorflow.keras import layers


class MyAntirectifier(layers.Layer):
    def build(self, input_shape):
        output_dim = input_shape[-1]
        self.kernel = self.add_weight(
            shape=(output_dim * 2, output_dim),
            initializer="he_normal",
            name="kernel",
            trainable=True,
        )

    def call(self, inputs):
        # Take the positive part of the input
        pos = tf.nn.relu(inputs)
        # Take the negative part of the input
        neg = tf.nn.relu(-inputs)
        # Concatenate the positive and negative parts
        concatenated = tf.concat([pos, neg], axis=0)
        # Project the concatenation down to the same dimensionality as the input
        return tf.matmul(concatenated, self.kernel)

Now, rather than using it in a end-to-end model directly, let's try to call the layer on some test data:

x = tf.random.normal(shape=(2, 5))
y = MyAntirectifier()(x)

We get the following error:

...
      1 x = tf.random.normal(shape=(2, 5))
----> 2 y = MyAntirectifier()(x)
...
     17         neg = tf.nn.relu(-inputs)
     18         concatenated = tf.concat([pos, neg], axis=0)
---> 19         return tf.matmul(concatenated, self.kernel)
...
InvalidArgumentError: Matrix size-incompatible: In[0]: [4,5], In[1]: [10,5] [Op:MatMul]

Looks like our input tensor in the matmul op may have an incorrect shape. Let's add a print statement to check the actual shapes:

class MyAntirectifier(layers.Layer):
    def build(self, input_shape):
        output_dim = input_shape[-1]
        self.kernel = self.add_weight(
            shape=(output_dim * 2, output_dim),
            initializer="he_normal",
            name="kernel",
            trainable=True,
        )

    def call(self, inputs):
        pos = tf.nn.relu(inputs)
        neg = tf.nn.relu(-inputs)
        print("pos.shape:", pos.shape)
        print("neg.shape:", neg.shape)
        concatenated = tf.concat([pos, neg], axis=0)
        print("concatenated.shape:", concatenated.shape)
        print("kernel.shape:", self.kernel.shape)
        return tf.matmul(concatenated, self.kernel)

We get the following:

pos.shape: (2, 5)
neg.shape: (2, 5)
concatenated.shape: (4, 5)
kernel.shape: (10, 5)

Turns out we had the wrong axis for the concat op! We should be concatenating neg and pos alongside the feature axis 1, not the batch axis 0. Here's the correct version:

class MyAntirectifier(layers.Layer):
    def build(self, input_shape):
        output_dim = input_shape[-1]
        self.kernel = self.add_weight(
            shape=(output_dim * 2, output_dim),
            initializer="he_normal",
            name="kernel",
            trainable=True,
        )

    def call(self, inputs):
        pos = tf.nn.relu(inputs)
        neg = tf.nn.relu(-inputs)
        print("pos.shape:", pos.shape)
        print("neg.shape:", neg.shape)
        concatenated = tf.concat([pos, neg], axis=1)
        print("concatenated.shape:", concatenated.shape)
        print("kernel.shape:", self.kernel.shape)
        return tf.matmul(concatenated, self.kernel)

Now our code works fine:

x = tf.random.normal(shape=(2, 5))
y = MyAntirectifier()(x)

pos.shape: (2, 5)
neg.shape: (2, 5)
concatenated.shape: (2, 10)
kernel.shape: (10, 5)

Tip 2: use model.summary() and plot_model() to check layer output shapes

If you're working with complex network topologies, you're going to need a way to visualize how your layers are connected and how they transform the data that passes through them.

Here's an example. Consider this model with three inputs and two outputs (lifted from the Functional API guide):

from tensorflow import keras

num_tags = 12  # Number of unique issue tags
num_words = 10000  # Size of vocabulary obtained when preprocessing text data
num_departments = 4  # Number of departments for predictions

title_input = keras.Input(
    shape=(None,), name="title"
)  # Variable-length sequence of ints
body_input = keras.Input(shape=(None,), name="body")  # Variable-length sequence of ints
tags_input = keras.Input(
    shape=(num_tags,), name="tags"
)  # Binary vectors of size `num_tags`

# Embed each word in the title into a 64-dimensional vector
title_features = layers.Embedding(num_words, 64)(title_input)
# Embed each word in the text into a 64-dimensional vector
body_features = layers.Embedding(num_words, 64)(body_input)

# Reduce sequence of embedded words in the title into a single 128-dimensional vector
title_features = layers.LSTM(128)(title_features)
# Reduce sequence of embedded words in the body into a single 32-dimensional vector
body_features = layers.LSTM(32)(body_features)

# Merge all available features into a single large vector via concatenation
x = layers.concatenate([title_features, body_features, tags_input])

# Stick a logistic regression for priority prediction on top of the features
priority_pred = layers.Dense(1, name="priority")(x)
# Stick a department classifier on top of the features
department_pred = layers.Dense(num_departments, name="department")(x)

# Instantiate an end-to-end model predicting both priority and department
model = keras.Model(
    inputs=[title_input, body_input, tags_input],
    outputs=[priority_pred, department_pred],
)

Calling summary() can help you check the output shape of each layer:

model.summary()

Model: "functional_1"
__________________________________________________________________________________________________
Layer (type)                    Output Shape         Param #     Connected to                     
==================================================================================================
title (InputLayer)              [(None, None)]       0                                            
__________________________________________________________________________________________________
body (InputLayer)               [(None, None)]       0                                            
__________________________________________________________________________________________________
embedding (Embedding)           (None, None, 64)     640000      title[0][0]                      
__________________________________________________________________________________________________
embedding_1 (Embedding)         (None, None, 64)     640000      body[0][0]                       
__________________________________________________________________________________________________
lstm (LSTM)                     (None, 128)          98816       embedding[0][0]                  
__________________________________________________________________________________________________
lstm_1 (LSTM)                   (None, 32)           12416       embedding_1[0][0]                
__________________________________________________________________________________________________
tags (InputLayer)               [(None, 12)]         0                                            
__________________________________________________________________________________________________
concatenate (Concatenate)       (None, 172)          0           lstm[0][0]                       
                                                                 lstm_1[0][0]                     
                                                                 tags[0][0]                       
__________________________________________________________________________________________________
priority (Dense)                (None, 1)            173         concatenate[0][0]                
__________________________________________________________________________________________________
department (Dense)              (None, 4)            692         concatenate[0][0]                
==================================================================================================
Total params: 1,392,097
Trainable params: 1,392,097
Non-trainable params: 0
__________________________________________________________________________________________________

You can also visualize the entire network topology alongside output shapes using plot_model:

keras.utils.plot_model(model, show_shapes=True)

png

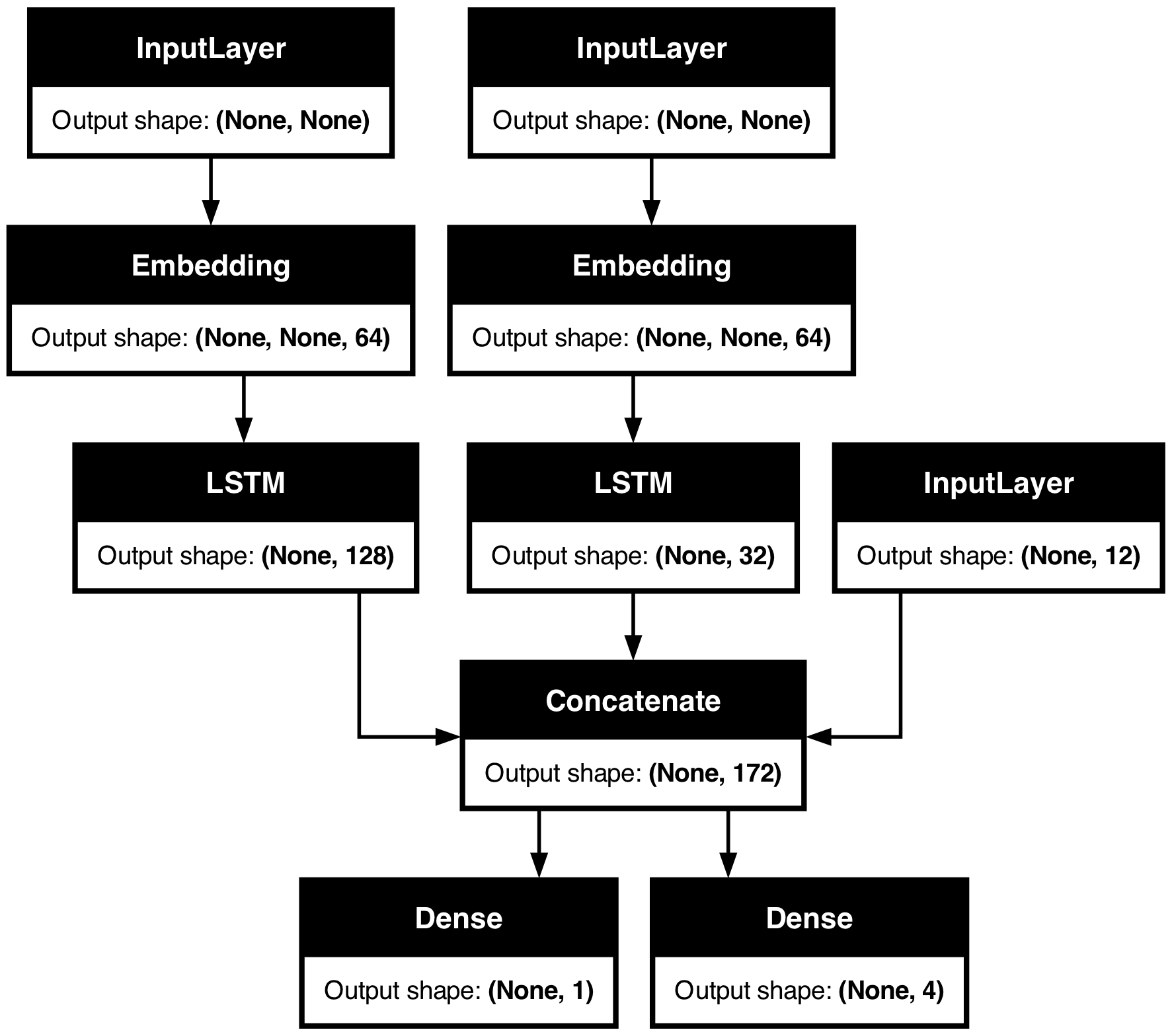
With this plot, any connectivity-level error becomes immediately obvious.

Tip 3: to debug what happens during fit(), use run_eagerly=True

The fit() method is fast: it runs a well-optimized, fully-compiled computation graph. That's great for performance, but it also means that the code you're executing isn't the Python code you've written. This can be problematic when debugging. As you may recall, Python is slow -- so we use it as a staging language, not as an execution language.

Thankfully, there's an easy way to run your code in "debug mode", fully eagerly: pass run_eagerly=True to compile(). Your call to fit() will now get executed line by line, without any optimization. It's slower, but it makes it possible to print the value of intermediate tensors, or to use a Python debugger. Great for debugging.

Here's a basic example: let's write a really simple model with a custom train_step. Our model just implements gradient descent, but instead of first-order gradients, it uses a combination of first-order and second-order gradients. Pretty trivial so far.

Can you spot what we're doing wrong?

class MyModel(keras.Model):
    def train_step(self, data):
        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                preds = self(inputs, training=True)  # Forward pass
                # Compute the loss value
                # (the loss function is configured in `compile()`)
                loss = self.compiled_loss(targets, preds)
            # Compute first-order gradients
            dl_dw = tape1.gradient(loss, trainable_vars)
        # Compute second-order gradients
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        # Combine first-order and second-order gradients
        grads = [0.5 * w1 + 0.5 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # Update weights
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # Update metrics (includes the metric that tracks the loss)
        self.compiled_metrics.update_state(targets, preds)
        # Return a dict mapping metric names to current value
        return {m.name: m.result() for m in self.metrics}

Let's train a one-layer model on MNIST with this custom training loop.

We pick, somewhat at random, a batch size of 1024 and a learning rate of 0.1. The general idea being to use larger batches and a larger learning rate than usual, since our "improved" gradients should lead us to quicker convergence.

import numpy as np

# Construct an instance of MyModel
def get_model():
    inputs = keras.Input(shape=(784,))
    intermediate = layers.Dense(256, activation="relu")(inputs)
    outputs = layers.Dense(10, activation="softmax")(intermediate)
    model = MyModel(inputs, outputs)
    return model


# Prepare data
(x_train, y_train), _ = keras.datasets.mnist.load_data()
x_train = np.reshape(x_train, (-1, 784)) / 255

model = get_model()
model.compile(
    optimizer=keras.optimizers.SGD(learning_rate=1e-2),
    loss="sparse_categorical_crossentropy",
    metrics=["accuracy"],
)
model.fit(x_train, y_train, epochs=3, batch_size=1024, validation_split=0.1)

Epoch 1/3
53/53 [==============================] - 1s 15ms/step - loss: 2.2960 - accuracy: 0.1580 - val_loss: 2.3071 - val_accuracy: 0.0963
Epoch 2/3
53/53 [==============================] - 1s 13ms/step - loss: 2.3246 - accuracy: 0.0995 - val_loss: 2.3454 - val_accuracy: 0.0960
Epoch 3/3
53/53 [==============================] - 1s 12ms/step - loss: 2.3578 - accuracy: 0.0995 - val_loss: 2.3767 - val_accuracy: 0.0960

<tensorflow.python.keras.callbacks.History at 0x151cbf0d0>

Oh no, it doesn't converge! Something is not working as planned.

Time for some step-by-step printing of what's going on with our gradients.

We add various print statements in the train_step method, and we make sure to pass run_eagerly=True to compile() to run our code step-by-step, eagerly.

class MyModel(keras.Model):
    def train_step(self, data):
        print()
        print("----Start of step: %d" % (self.step_counter,))
        self.step_counter += 1

        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                preds = self(inputs, training=True)  # Forward pass
                # Compute the loss value
                # (the loss function is configured in `compile()`)
                loss = self.compiled_loss(targets, preds)
            # Compute first-order gradients
            dl_dw = tape1.gradient(loss, trainable_vars)
        # Compute second-order gradients
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        print("Max of dl_dw[0]: %.4f" % tf.reduce_max(dl_dw[0]))
        print("Min of dl_dw[0]: %.4f" % tf.reduce_min(dl_dw[0]))
        print("Mean of dl_dw[0]: %.4f" % tf.reduce_mean(dl_dw[0]))
        print("-")
        print("Max of d2l_dw2[0]: %.4f" % tf.reduce_max(d2l_dw2[0]))
        print("Min of d2l_dw2[0]: %.4f" % tf.reduce_min(d2l_dw2[0]))
        print("Mean of d2l_dw2[0]: %.4f" % tf.reduce_mean(d2l_dw2[0]))

        # Combine first-order and second-order gradients
        grads = [0.5 * w1 + 0.5 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # Update weights
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # Update metrics (includes the metric that tracks the loss)
        self.compiled_metrics.update_state(targets, preds)
        # Return a dict mapping metric names to current value
        return {m.name: m.result() for m in self.metrics}


model = get_model()
model.compile(
    optimizer=keras.optimizers.SGD(learning_rate=1e-2),
    loss="sparse_categorical_crossentropy",
    metrics=["accuracy"],
    run_eagerly=True,
)
model.step_counter = 0
# We pass epochs=1 and steps_per_epoch=10 to only run 10 steps of training.
model.fit(x_train, y_train, epochs=1, batch_size=1024, verbose=0, steps_per_epoch=10)

----Start of step: 0
Max of dl_dw[0]: 0.0236
Min of dl_dw[0]: -0.0198
Mean of dl_dw[0]: 0.0001
-
Max of d2l_dw2[0]: 2.6148
Min of d2l_dw2[0]: -1.8798
Mean of d2l_dw2[0]: 0.0401

----Start of step: 1
Max of dl_dw[0]: 0.0611
Min of dl_dw[0]: -0.0233
Mean of dl_dw[0]: 0.0009
-
Max of d2l_dw2[0]: 8.3185
Min of d2l_dw2[0]: -4.0696
Mean of d2l_dw2[0]: 0.1708

----Start of step: 2
Max of dl_dw[0]: 0.0528
Min of dl_dw[0]: -0.0200
Mean of dl_dw[0]: 0.0010
-
Max of d2l_dw2[0]: 3.4744
Min of d2l_dw2[0]: -3.1926
Mean of d2l_dw2[0]: 0.0559

----Start of step: 3
Max of dl_dw[0]: 0.0983
Min of dl_dw[0]: -0.0174
Mean of dl_dw[0]: 0.0014
-
Max of d2l_dw2[0]: 2.2682
Min of d2l_dw2[0]: -0.7935
Mean of d2l_dw2[0]: 0.0253

----Start of step: 4
Max of dl_dw[0]: 0.0732
Min of dl_dw[0]: -0.0125
Mean of dl_dw[0]: 0.0009
-
Max of d2l_dw2[0]: 5.1099
Min of d2l_dw2[0]: -2.4236
Mean of d2l_dw2[0]: 0.0860

----Start of step: 5
Max of dl_dw[0]: 0.1309
Min of dl_dw[0]: -0.0103
Mean of dl_dw[0]: 0.0007
-
Max of d2l_dw2[0]: 5.1275
Min of d2l_dw2[0]: -0.6684
Mean of d2l_dw2[0]: 0.0349

----Start of step: 6
Max of dl_dw[0]: 0.0484
Min of dl_dw[0]: -0.0128
Mean of dl_dw[0]: 0.0001
-
Max of d2l_dw2[0]: 5.3465
Min of d2l_dw2[0]: -0.2145
Mean of d2l_dw2[0]: 0.0618

----Start of step: 7
Max of dl_dw[0]: 0.0049
Min of dl_dw[0]: -0.0093
Mean of dl_dw[0]: -0.0001
-
Max of d2l_dw2[0]: 0.2465
Min of d2l_dw2[0]: -0.0313
Mean of d2l_dw2[0]: 0.0075

----Start of step: 8
Max of dl_dw[0]: 0.0050
Min of dl_dw[0]: -0.0120
Mean of dl_dw[0]: -0.0001
-
Max of d2l_dw2[0]: 0.1978
Min of d2l_dw2[0]: -0.0291
Mean of d2l_dw2[0]: 0.0063

----Start of step: 9
Max of dl_dw[0]: 0.0050
Min of dl_dw[0]: -0.0125
Mean of dl_dw[0]: -0.0001
-
Max of d2l_dw2[0]: 0.1594
Min of d2l_dw2[0]: -0.0238
Mean of d2l_dw2[0]: 0.0055

<tensorflow.python.keras.callbacks.History at 0x17f65f410>

What did we learn?

  • The first order and second order gradients can have values that differ by orders of magnitudes.
  • Sometimes, they may not even have the same sign.
  • Their values can vary greatly at each step.

This leads us to an obvious idea: let's normalize the gradients before combining them.

class MyModel(keras.Model):
    def train_step(self, data):
        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                preds = self(inputs, training=True)  # Forward pass
                # Compute the loss value
                # (the loss function is configured in `compile()`)
                loss = self.compiled_loss(targets, preds)
            # Compute first-order gradients
            dl_dw = tape1.gradient(loss, trainable_vars)
        # Compute second-order gradients
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        dl_dw = [tf.math.l2_normalize(w) for w in dl_dw]
        d2l_dw2 = [tf.math.l2_normalize(w) for w in d2l_dw2]

        # Combine first-order and second-order gradients
        grads = [0.5 * w1 + 0.5 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # Update weights
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # Update metrics (includes the metric that tracks the loss)
        self.compiled_metrics.update_state(targets, preds)
        # Return a dict mapping metric names to current value
        return {m.name: m.result() for m in self.metrics}


model = get_model()
model.compile(
    optimizer=keras.optimizers.SGD(learning_rate=1e-2),
    loss="sparse_categorical_crossentropy",
    metrics=["accuracy"],
)
model.fit(x_train, y_train, epochs=5, batch_size=1024, validation_split=0.1)

Epoch 1/5
53/53 [==============================] - 1s 15ms/step - loss: 2.1680 - accuracy: 0.2796 - val_loss: 2.0063 - val_accuracy: 0.4688
Epoch 2/5
53/53 [==============================] - 1s 13ms/step - loss: 1.9071 - accuracy: 0.5292 - val_loss: 1.7729 - val_accuracy: 0.6312
Epoch 3/5
53/53 [==============================] - 1s 13ms/step - loss: 1.7098 - accuracy: 0.6197 - val_loss: 1.5966 - val_accuracy: 0.6785
Epoch 4/5
53/53 [==============================] - 1s 13ms/step - loss: 1.5686 - accuracy: 0.6434 - val_loss: 1.4748 - val_accuracy: 0.6875
Epoch 5/5
53/53 [==============================] - 1s 14ms/step - loss: 1.4729 - accuracy: 0.6448 - val_loss: 1.3908 - val_accuracy: 0.6862

<tensorflow.python.keras.callbacks.History at 0x1a1105210>

Now, training converges! It doesn't work well at all, but at least the model learns something.

After spending a few minutes tuning parameters, we get to the following configuration that works somewhat well (achieves 97% validation accuracy and seems reasonably robust to overfitting):

  • Use 0.2 * w1 + 0.8 * w2 for combining gradients.
  • Use a learning rate that decays linearly over time.

I'm not going to say that the idea works -- this isn't at all how you're supposed to do second-order optimization (pointers: see the Newton & Gauss-Newton methods, quasi-Newton methods, and BFGS). But hopefully this demonstration gave you an idea of how you can debug your way out of uncomfortable training situations.

Remember: use run_eagerly=True for debugging what happens in fit(). And when your code is finally working as expected, make sure to remove this flag in order to get the best runtime performance!

Here's our final training run:

class MyModel(keras.Model):
    def train_step(self, data):
        inputs, targets = data
        trainable_vars = self.trainable_variables
        with tf.GradientTape() as tape2:
            with tf.GradientTape() as tape1:
                preds = self(inputs, training=True)  # Forward pass
                # Compute the loss value
                # (the loss function is configured in `compile()`)
                loss = self.compiled_loss(targets, preds)
            # Compute first-order gradients
            dl_dw = tape1.gradient(loss, trainable_vars)
        # Compute second-order gradients
        d2l_dw2 = tape2.gradient(dl_dw, trainable_vars)

        dl_dw = [tf.math.l2_normalize(w) for w in dl_dw]
        d2l_dw2 = [tf.math.l2_normalize(w) for w in d2l_dw2]

        # Combine first-order and second-order gradients
        grads = [0.2 * w1 + 0.8 * w2 for (w1, w2) in zip(d2l_dw2, dl_dw)]

        # Update weights
        self.optimizer.apply_gradients(zip(grads, trainable_vars))

        # Update metrics (includes the metric that tracks the loss)
        self.compiled_metrics.update_state(targets, preds)
        # Return a dict mapping metric names to current value
        return {m.name: m.result() for m in self.metrics}


model = get_model()
lr = learning_rate = keras.optimizers.schedules.InverseTimeDecay(
    initial_learning_rate=0.1, decay_steps=25, decay_rate=0.1
)
model.compile(
    optimizer=keras.optimizers.SGD(lr),
    loss="sparse_categorical_crossentropy",
    metrics=["accuracy"],
)
model.fit(x_train, y_train, epochs=50, batch_size=2048, validation_split=0.1)

Epoch 1/50
27/27 [==============================] - 1s 31ms/step - loss: 1.3838 - accuracy: 0.6598 - val_loss: 0.6603 - val_accuracy: 0.8688
Epoch 2/50
27/27 [==============================] - 1s 29ms/step - loss: 0.5872 - accuracy: 0.8547 - val_loss: 0.4188 - val_accuracy: 0.8977
Epoch 3/50
27/27 [==============================] - 1s 31ms/step - loss: 0.4481 - accuracy: 0.8782 - val_loss: 0.3434 - val_accuracy: 0.9113
Epoch 4/50
27/27 [==============================] - 1s 32ms/step - loss: 0.3857 - accuracy: 0.8933 - val_loss: 0.3149 - val_accuracy: 0.9115
Epoch 5/50
27/27 [==============================] - 1s 30ms/step - loss: 0.3482 - accuracy: 0.9020 - val_loss: 0.2752 - val_accuracy: 0.9248
Epoch 6/50
27/27 [==============================] - 1s 34ms/step - loss: 0.3219 - accuracy: 0.9091 - val_loss: 0.2549 - val_accuracy: 0.9287
Epoch 7/50
27/27 [==============================] - 1s 30ms/step - loss: 0.3023 - accuracy: 0.9147 - val_loss: 0.2480 - val_accuracy: 0.9305
Epoch 8/50
27/27 [==============================] - 1s 33ms/step - loss: 0.2866 - accuracy: 0.9188 - val_loss: 0.2327 - val_accuracy: 0.9362
Epoch 9/50
27/27 [==============================] - 1s 39ms/step - loss: 0.2733 - accuracy: 0.9228 - val_loss: 0.2226 - val_accuracy: 0.9383
Epoch 10/50
27/27 [==============================] - 1s 33ms/step - loss: 0.2613 - accuracy: 0.9267 - val_loss: 0.2147 - val_accuracy: 0.9420
Epoch 11/50
27/27 [==============================] - 1s 34ms/step - loss: 0.2509 - accuracy: 0.9294 - val_loss: 0.2049 - val_accuracy: 0.9447
Epoch 12/50
27/27 [==============================] - 1s 32ms/step - loss: 0.2417 - accuracy: 0.9324 - val_loss: 0.1978 - val_accuracy: 0.9455
Epoch 13/50
27/27 [==============================] - 1s 32ms/step - loss: 0.2330 - accuracy: 0.9345 - val_loss: 0.1906 - val_accuracy: 0.9488
Epoch 14/50
27/27 [==============================] - 1s 34ms/step - loss: 0.2252 - accuracy: 0.9372 - val_loss: 0.1853 - val_accuracy: 0.9508
Epoch 15/50
27/27 [==============================] - 1s 34ms/step - loss: 0.2184 - accuracy: 0.9392 - val_loss: 0.1805 - val_accuracy: 0.9523
Epoch 16/50
27/27 [==============================] - 1s 38ms/step - loss: 0.2113 - accuracy: 0.9413 - val_loss: 0.1760 - val_accuracy: 0.9518
Epoch 17/50
27/27 [==============================] - 1s 38ms/step - loss: 0.2055 - accuracy: 0.9427 - val_loss: 0.1709 - val_accuracy: 0.9552
Epoch 18/50
27/27 [==============================] - 1s 42ms/step - loss: 0.1998 - accuracy: 0.9441 - val_loss: 0.1669 - val_accuracy: 0.9567
Epoch 19/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1944 - accuracy: 0.9458 - val_loss: 0.1625 - val_accuracy: 0.9577
Epoch 20/50
27/27 [==============================] - 1s 33ms/step - loss: 0.1891 - accuracy: 0.9471 - val_loss: 0.1580 - val_accuracy: 0.9585
Epoch 21/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1846 - accuracy: 0.9484 - val_loss: 0.1564 - val_accuracy: 0.9603
Epoch 22/50
27/27 [==============================] - 1s 41ms/step - loss: 0.1804 - accuracy: 0.9498 - val_loss: 0.1518 - val_accuracy: 0.9622
Epoch 23/50
27/27 [==============================] - 1s 38ms/step - loss: 0.1762 - accuracy: 0.9507 - val_loss: 0.1485 - val_accuracy: 0.9628
Epoch 24/50
27/27 [==============================] - 1s 41ms/step - loss: 0.1722 - accuracy: 0.9521 - val_loss: 0.1461 - val_accuracy: 0.9623
Epoch 25/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1686 - accuracy: 0.9534 - val_loss: 0.1434 - val_accuracy: 0.9633
Epoch 26/50
27/27 [==============================] - 1s 35ms/step - loss: 0.1652 - accuracy: 0.9542 - val_loss: 0.1419 - val_accuracy: 0.9637
Epoch 27/50
27/27 [==============================] - 1s 34ms/step - loss: 0.1618 - accuracy: 0.9550 - val_loss: 0.1397 - val_accuracy: 0.9633
Epoch 28/50
27/27 [==============================] - 1s 35ms/step - loss: 0.1589 - accuracy: 0.9556 - val_loss: 0.1371 - val_accuracy: 0.9647
Epoch 29/50
27/27 [==============================] - 1s 37ms/step - loss: 0.1561 - accuracy: 0.9566 - val_loss: 0.1350 - val_accuracy: 0.9650
Epoch 30/50
27/27 [==============================] - 1s 41ms/step - loss: 0.1534 - accuracy: 0.9574 - val_loss: 0.1331 - val_accuracy: 0.9655
Epoch 31/50
27/27 [==============================] - 1s 39ms/step - loss: 0.1508 - accuracy: 0.9583 - val_loss: 0.1319 - val_accuracy: 0.9660
Epoch 32/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1484 - accuracy: 0.9589 - val_loss: 0.1314 - val_accuracy: 0.9667
Epoch 33/50
27/27 [==============================] - 1s 39ms/step - loss: 0.1463 - accuracy: 0.9597 - val_loss: 0.1290 - val_accuracy: 0.9668
Epoch 34/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1439 - accuracy: 0.9600 - val_loss: 0.1268 - val_accuracy: 0.9675
Epoch 35/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1418 - accuracy: 0.9608 - val_loss: 0.1256 - val_accuracy: 0.9677
Epoch 36/50
27/27 [==============================] - 1s 38ms/step - loss: 0.1397 - accuracy: 0.9614 - val_loss: 0.1245 - val_accuracy: 0.9685
Epoch 37/50
27/27 [==============================] - 1s 35ms/step - loss: 0.1378 - accuracy: 0.9625 - val_loss: 0.1223 - val_accuracy: 0.9683
Epoch 38/50
27/27 [==============================] - 1s 38ms/step - loss: 0.1362 - accuracy: 0.9620 - val_loss: 0.1216 - val_accuracy: 0.9695
Epoch 39/50
27/27 [==============================] - 1s 38ms/step - loss: 0.1344 - accuracy: 0.9628 - val_loss: 0.1207 - val_accuracy: 0.9685
Epoch 40/50
27/27 [==============================] - 1s 37ms/step - loss: 0.1327 - accuracy: 0.9634 - val_loss: 0.1192 - val_accuracy: 0.9692
Epoch 41/50
27/27 [==============================] - 1s 41ms/step - loss: 0.1309 - accuracy: 0.9635 - val_loss: 0.1179 - val_accuracy: 0.9695
Epoch 42/50
27/27 [==============================] - 1s 39ms/step - loss: 0.1294 - accuracy: 0.9641 - val_loss: 0.1173 - val_accuracy: 0.9695
Epoch 43/50
27/27 [==============================] - 1s 41ms/step - loss: 0.1281 - accuracy: 0.9646 - val_loss: 0.1160 - val_accuracy: 0.9705
Epoch 44/50
27/27 [==============================] - 1s 42ms/step - loss: 0.1265 - accuracy: 0.9650 - val_loss: 0.1158 - val_accuracy: 0.9700
Epoch 45/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1251 - accuracy: 0.9654 - val_loss: 0.1149 - val_accuracy: 0.9695
Epoch 46/50
27/27 [==============================] - 1s 39ms/step - loss: 0.1237 - accuracy: 0.9658 - val_loss: 0.1140 - val_accuracy: 0.9700
Epoch 47/50
27/27 [==============================] - 1s 40ms/step - loss: 0.1224 - accuracy: 0.9664 - val_loss: 0.1128 - val_accuracy: 0.9707
Epoch 48/50
27/27 [==============================] - 1s 38ms/step - loss: 0.1211 - accuracy: 0.9664 - val_loss: 0.1122 - val_accuracy: 0.9710
Epoch 49/50
27/27 [==============================] - 1s 39ms/step - loss: 0.1198 - accuracy: 0.9670 - val_loss: 0.1114 - val_accuracy: 0.9713
Epoch 50/50
27/27 [==============================] - 1s 45ms/step - loss: 0.1186 - accuracy: 0.9677 - val_loss: 0.1106 - val_accuracy: 0.9703

<tensorflow.python.keras.callbacks.History at 0x1b79ec350>

Tip 4: if your code is slow, run the TensorFlow profiler

One last tip -- if your code seems slower than it should be, you're going to want to plot how much time is spent on each computation step. Look for any bottleneck that might be causing less than 100% device utilization.

To learn more about TensorFlow profiling, see this extensive guide.

You can quickly profile a Keras model via the TensorBoard callback:

# Profile from batches 10 to 15
tb_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir,
                                             profile_batch=(10, 15))
# Train the model and use the TensorBoard Keras callback to collect
# performance profiling data
model.fit(dataset,
          epochs=1,
          callbacks=[tb_callback])

Then navigate to the TensorBoard app and check the "profile" tab.

Keras debugging tips
◆ Introduction
◆ Tip 1: test each part before you test the whole
◆ Tip 2: use model.summary() and plot_model() to check layer output shapes
◆ Tip 3: to debug what happens during fit(), use run_eagerly=True
◆ Tip 4: if your code is slow, run the TensorFlow profiler